Dijkstra算法C语言实现
Dijkstra算法是一种用于寻找图中从单一源点到所有其他顶点的最短路径的算法,下面是一个完整的C语言实现,包括优先队列(最小堆)来优化性能。
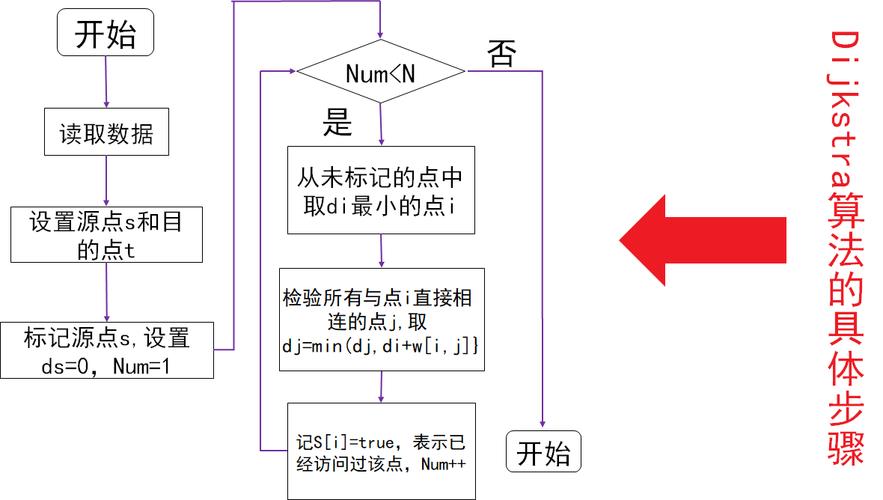
(图片来源网络,侵删)
完整实现代码
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// 图的结构体表示
typedef struct {
int V; // 顶点数
int **adj; // 邻接矩阵
} Graph;
// 最小堆节点结构体
typedef struct MinHeapNode {
int v; // 顶点索引
int dist; // 从源点到该顶点的距离
} MinHeapNode;
// 最小堆结构体
typedef struct MinHeap {
int size; // 当前堆大小
int capacity; // 堆容量
int *pos; // 存储顶点在堆中的位置
MinHeapNode **array; // 堆数组
} MinHeap;
// 创建图
Graph* createGraph(int V) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->V = V;
// 分配邻接矩阵内存
graph->adj = (int**)malloc(V * sizeof(int*));
for (int i = 0; i < V; i++) {
graph->adj[i] = (int*)malloc(V * sizeof(int));
for (int j = 0; j < V; j++) {
graph->adj[i][j] = 0;
}
}
return graph;
}
// 添加边到图中
void addEdge(Graph* graph, int src, int dest, int weight) {
graph->adj[src][dest] = weight;
graph->adj[dest][src] = weight; // 无向图
}
// 创建最小堆节点
MinHeapNode* newMinHeapNode(int v, int dist) {
MinHeapNode* node = (MinHeapNode*)malloc(sizeof(MinHeapNode));
node->v = v;
node->dist = dist;
return node;
}
// 创建最小堆
MinHeap* createMinHeap(int capacity) {
MinHeap* heap = (MinHeap*)malloc(sizeof(MinHeap));
heap->pos = (int*)malloc(capacity * sizeof(int));
heap->size = 0;
heap->capacity = capacity;
heap->array = (MinHeapNode**)malloc(capacity * sizeof(MinHeapNode*));
return heap;
}
// 交换两个堆节点
void swapMinHeapNode(MinHeapNode** a, MinHeapNode** b) {
MinHeapNode* t = *a;
*a = *b;
*b = t;
}
// 堆化函数
void minHeapify(MinHeap* heap, int idx) {
int smallest, left, right;
smallest = idx;
left = 2 * idx + 1;
right = 2 * idx + 2;
if (left < heap->size && heap->array[left]->dist < heap->array[smallest]->dist)
smallest = left;
if (right < heap->size && heap->array[right]->dist < heap->array[smallest]->dist)
smallest = right;
if (smallest != idx) {
// 交换节点在堆中的位置
MinHeapNode* smallestNode = heap->array[smallest];
MinHeapNode* idxNode = heap->array[idx];
heap->pos[smallestNode->v] = idx;
heap->pos[idxNode->v] = smallest;
swapMinHeapNode(&heap->array[smallest], &heap->array[idx]);
minHeapify(heap, smallest);
}
}
// 检查堆是否为空
int isEmpty(MinHeap* heap) {
return heap->size == 0;
}
// 提取最小节点
MinHeapNode* extractMin(MinHeap* heap) {
if (isEmpty(heap))
return NULL;
// 存储根节点
MinHeapNode* root = heap->array[0];
// 用最后一个节点替换根节点
MinHeapNode* lastNode = heap->array[heap->size - 1];
heap->array[0] = lastNode;
// 更新位置
heap->pos[root->v] = heap->size - 1;
heap->pos[lastNode->v] = 0;
// 减少堆大小并堆化
--heap->size;
minHeapify(heap, 0);
return root;
}
// 减少堆中某个节点的距离值
void decreaseKey(MinHeap* heap, int v, int dist) {
int i = heap->pos[v];
heap->array[i]->dist = dist;
// 向上调整堆
while (i != 0 && heap->array[i]->dist < heap->array[(i - 1) / 2]->dist) {
// 交换节点在堆中的位置
MinHeapNode* currentNode = heap->array[i];
MinHeapNode* parentNode = heap->array[(i - 1) / 2];
heap->pos[currentNode->v] = (i - 1) / 2;
heap->pos[parentNode->v] = i;
swapMinHeapNode(&heap->array[i], &heap->array[(i - 1) / 2]);
i = (i - 1) / 2;
}
}
// 检查顶点是否在堆中
bool isInMinHeap(MinHeap* heap, int v) {
if (heap->pos[v] < heap->size)
return true;
return false;
}
// 打印从源点到所有顶点的最短路径
void printArr(int dist[], int n) {
printf("Vertex Distance from Source\n");
for (int i = 0; i < n; ++i)
printf("%d \t\t %d\n", i, dist[i]);
}
// Dijkstra算法主函数
void dijkstra(Graph* graph, int src) {
int V = graph->V;
int dist[V]; // 存储从源点到各顶点的最短距离
// 创建最小堆
MinHeap* heap = createMinHeap(V);
// 初始化距离和堆
for (int v = 0; v < V; ++v) {
dist[v] = INT_MAX;
heap->array[v] = newMinHeapNode(v, dist[v]);
heap->pos[v] = v;
}
// 源点到自身的距离为0
dist[src] = 0;
decreaseKey(heap, src, dist[src]);
// 初始堆大小为V
heap->size = V;
// 当堆不为空时
while (!isEmpty(heap)) {
// 提取最小距离的顶点
MinHeapNode* minHeapNode = extractMin(heap);
int u = minHeapNode->v;
// 遍历所有邻接顶点
for (int v = 0; v < V; ++v) {
if (graph->adj[u][v] && isInMinHeap(heap, v) &&
dist[u] != INT_MAX && dist[u] + graph->adj[u][v] < dist[v]) {
dist[v] = dist[u] + graph->adj[u][v];
decreaseKey(heap, v, dist[v]);
}
}
}
// 打印结果
printArr(dist, V);
}
// 主函数
int main() {
// 创建图
int V = 9;
Graph* graph = createGraph(V);
addEdge(graph, 0, 1, 4);
addEdge(graph, 0, 7, 8);
addEdge(graph, 1, 2, 8);
addEdge(graph, 1, 7, 11);
addEdge(graph, 2, 3, 7);
addEdge(graph, 2, 8, 2);
addEdge(graph, 2, 5, 4);
addEdge(graph, 3, 4, 9);
addEdge(graph, 3, 5, 14);
addEdge(graph, 4, 5, 10);
addEdge(graph, 5, 6, 2);
addEdge(graph, 6, 7, 1);
addEdge(graph, 6, 8, 6);
addEdge(graph, 7, 8, 7);
dijkstra(graph, 0);
return 0;
}
代码说明
-
数据结构:
Graph: 使用邻接矩阵表示图MinHeapNode: 表示堆中的节点,包含顶点索引和距离值MinHeap: 最小堆实现,用于高效获取当前距离最小的顶点
-
主要函数:
createGraph: 创建图结构addEdge: 添加边到图中dijkstra: Dijkstra算法主实现minHeapify: 维护堆性质extractMin: 提取堆中最小元素decreaseKey: 减少堆中某个节点的距离值
-
算法流程:
- 初始化所有顶点的距离为无穷大,源点距离为0
- 将所有顶点加入最小堆
- 循环从堆中提取距离最小的顶点
- 更新其所有邻接顶点的距离值
- 重复直到堆为空
-
时间复杂度:
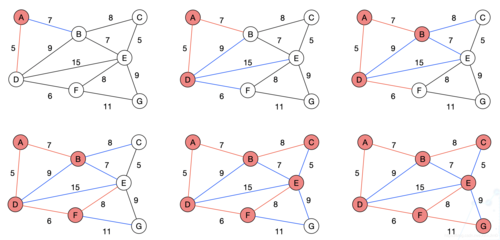 (图片来源网络,侵删)
(图片来源网络,侵删)使用优先队列(最小堆)实现的Dijkstra算法时间复杂度为O(E log V),其中E是边数,V是顶点数
示例输出
对于给定的图,程序输出如下:
Vertex Distance from Source
0 0
1 4
2 12
3 19
4 21
5 11
6 9
7 8
8 14这表示从顶点0出发到其他各顶点的最短距离。
(图片来源网络,侵删)




