prim算法求最小生成树c语言-C语言-盈思创科技

Prim 算法简介

Prim 算法是一种用于求解无向连通图最小生成树的贪心算法。

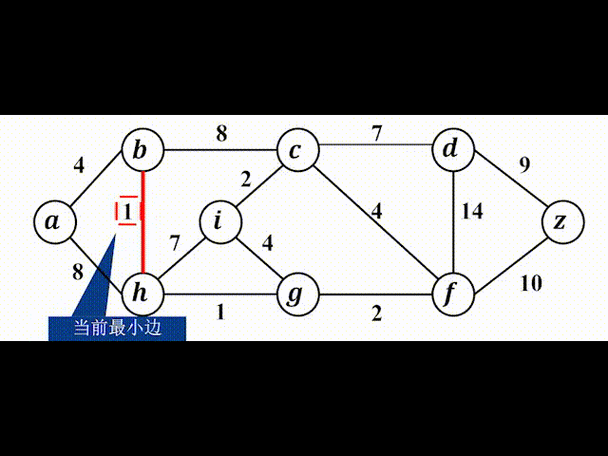
（图片来源网络，侵删）

核心思想： 从一个起始顶点开始，不断地将与当前生成树连接的、权重最小的边加入到生成树中,直到图中所有顶点都包含在生成树中。

算法步骤：

初始化：选择任意一个顶点作为起始点，将其加入生成树集合 U，所有其他顶点都在未加入集合 V-U 中。
选择最小边：在连接集合 U 和 V-U 的所有边中，找到权重最小的边 (u, v)，u 在 U 中，v 在 V-U 中。
更新集合：将这条最小边 (u, v) 加入到最小生成树的边集合中，并将顶点 v 从 V-U 移动到 U 中。
重复：重复步骤 2 和 3，直到 U 包含了图中的所有顶点。

数据结构选择

为了高效地实现“找到连接 U 和 V-U 的最小权重边”这一步，我们通常使用优先队列（最小堆），但在 C 语言中，标准库没有现成的优先队列,我们可以用数组来模拟。

这里我们采用一种更直观且易于理解的方法,使用三个辅助数组：

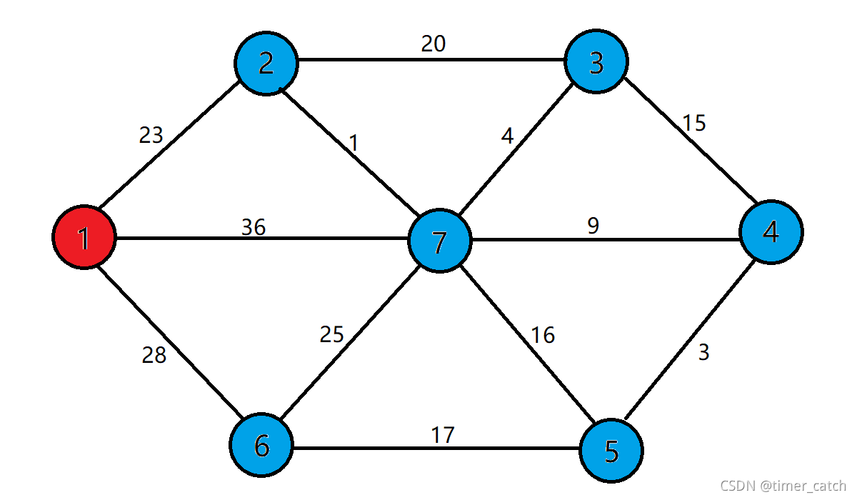
（图片来源网络，侵删）

lowcost[]: 记录每个顶点到生成树 U 的最小边的权重。lowcost[v] == 0，表示顶点 v 已经在 U 中。
closest[]: 记录每个顶点到生成树 U 的最小边所连接的 U 中的顶点。closest[v] == -1，表示顶点 v 尚未处理。
visited[]: 标记顶点是否已经被加入到生成树 U 中（与 lowcost[v] == 0 等价，但逻辑更清晰）。

C 语言代码实现

下面是一个完整的、带有详细注释的 C 语言实现。

#include <stdio.h>
#include <limits.h> // 用于 INT_MAX
#define MAX_VERTICES 100 // 最大顶点数
#define INF INT_MAX      // 表示无穷大（不相连）
// 图的结构体，使用邻接矩阵表示
typedef struct {
    int numVertices;           // 顶点数
    int adjacencyMatrix[MAX_VERTICES][MAX_VERTICES]; // 邻接矩阵
} Graph;
/**
 * @brief 使用 Prim 算法查找并打印最小生成树
 * @param graph 图的指针
 * @param startVertex 起始顶点的索引
 */
void primMST(Graph* graph, int startVertex) {
    int numV = graph->numVertices;
    // --- 辅助数组 ---
    int lowcost[MAX_VERTICES]; // lowcost[i] = 顶点i到U的最小权重
    int closest[MAX_VERTICES]; // closest[i] = 与顶点i相连的U中的顶点
    int visited[MAX_VERTICES]; // visited[i] = 1 if vertex i is in U, 0 otherwise
    // 1. 初始化
    for (int i = 0; i < numV; i++) {
        lowcost[i] = graph->adjacencyMatrix[startVertex][i];
        closest[i] = startVertex;
        visited[i] = 0;
    }
    // 将起始顶点标记为已访问
    visited[startVertex] = 1;
    closest[startVertex] = -1; // 起始顶点没有“最近的”U中的顶点
    printf("Minimum Spanning Tree (Prim's Algorithm):\n");
    printf("Edge \tWeight\n");
    int totalWeight = 0;
    // 2. 循环 n-1 次，因为 MST 有 n-1 条边
    for (int i = 1; i < numV; i++) {
        int minWeight = INF;
        int v = -1; // 将要加入U的顶点
        // 3. 在 V-U 集合中，找到 lowcost 值最小的顶点 v
        for (int j = 0; j < numV; j++) {
            if (!visited[j] && lowcost[j] < minWeight) {
                minWeight = lowcost[j];
                v = j;
            }
        }
        // 如果找不到这样的顶点，说明图不连通
        if (v == -1) {
            printf("Graph is not connected. MST cannot be formed.\n");
            return;
        }
        // 4. 将顶点 v 加入 U
        visited[v] = 1;
        // 5. 打印找到的边和权重
        printf("%d - %d \t%d\n", closest[v], v, minWeight);
        totalWeight += minWeight;
        // 6. 更新 lowcost 和 closest 数组
        // 对于所有未访问的顶点 j，检查从新加入的 v 到 j 的边是否比之前记录的更小
        for (int j = 0; j < numV; j++) {
            if (!visited[j] && graph->adjacencyMatrix[v][j] < lowcost[j]) {
                lowcost[j] = graph->adjacencyMatrix[v][j];
                closest[j] = v;
            }
        }
    }
    printf("------------------------------------\n");
    printf("Total Weight of MST: %d\n", totalWeight);
}
int main() {
    // 创建一个图实例
    Graph g;
    // 示例图 (9个顶点)
    //       (0)
    //      /   \
    //   (1)/     \(5)
    //    /       \
    // (2)---(3)---(4)
    //  | \   |   / |
    // (6)| \(7)/ |(8)
    //   |   \|/   |
    //   (5)---(6)
    // 注意：为了演示，我们使用了 0-8 的顶点编号，但实际顶点数是 7
    // 这里我们重新定义一个更清晰的 6 顶点图
    // 重新定义一个更清晰的 6 顶点图
    /*
       0 -- 1 -- 2
       |  / |  / |
       | /  | /  |
       3 -- 4 -- 5
    */
    g.numVertices = 6;
    // 初始化邻接矩阵为无穷大
    for (int i =  ㅠ0; i < g.numVertices; i++) {
        for (int j = 0; j < g.numVertices; j++) {
            g.adjacencyMatrix[i][j] = INF;
        }
    }
    // 添加边（无向图，所以对称赋值）
    g.adjacencyMatrix[0][1] = 4; g.adjacencyMatrix[1][0] = 4;
    g.adjacencyMatrix[0][3] = 1; g.adjacencyMatrix[3][0] = 1;
    g.adjacencyMatrix[1][2] = 1; g.adjacencyMatrix[2][1] = 1;
    g.adjacencyMatrix[1][3] = 3; g.adjacencyMatrix[3][1] = 3;
    g.adjacencyMatrix[1][4] = 2; g.adjacencyMatrix[4][1] = 2;
    g.adjacencyMatrix[2][4] = 5; g.adjacencyMatrix[4][2] = 5;
    g.adjacencyMatrix[3][4] = 8; g.adjacencyMatrix[4][3] = 8;
    g.adjacencyMatrix[3][5] = 7; g.adjacencyMatrix[5][3] = 7;
    g.adjacencyMatrix[4][5] = 6; g.adjacencyMatrix[5][4] = 6;
    printf("Graph Adjacency Matrix:\n");
    for (int i = 0; i < g.numVertices; i++) {
        for (int j = 0; j < g.numVertices; j++) {
            if (g.adjacencyMatrix[i][j] == INF) {
                printf("INF ");
            } else {
                printf("%-4d ", g.adjacencyMatrix[i][j]);
            }
        }
        printf("\n");
    }
    printf("\n");
    // 从顶点 0 开始运行 Prim 算法
    primMST(&g, 0);
    return 0;
}

代码解析

Graph 结构体：使用邻接矩阵 adjacencyMatrix 来存储图。adjacencyMatrix[i][j] 的值代表顶点 i 和 j 之间的边的权重，如果两个顶点不直接相连，则权重为 INF（无穷大）。
primMST 函数：
- 初始化：在函数开始时，我们创建并初始化三个辅助数组 lowcost, closest, 和 visited。
  - lowcost 和 closest 的初始值都基于 startVertex。lowcost[1] 是 startVertex 到顶点 1 的权重。
  - visited[startVertex] 被设为 1,表示起始点已经加入生成树。
- 主循环：循环 numV - 1 次，因为 MST 的边数总是顶点数减一。
- 寻找最小边：在每次循环中，遍历所有未访问的顶点，找到 lowcost 值最小的那个顶点 v，这个 v 就是下一个要加入生成树的顶点。
- 更新和打印：将 v 标记为已访问，然后打印连接 v 和 closest[v] 的边及其权重。closest[v] 正是这条最小边在生成树中的另一个端点。
- 更新数组：这是最关键的一步，将 v 加入 U 后，v 就可以作为“跳板”了，我们遍历所有未访问的顶点 j，检查从 v 到 j 的边权重是否比 j 当前的 lowcost 值更小，如果是，则更新 lowcost[j] 和 closest[j]，这确保了 lowcost 数组始终保存了每个顶点到 U 的最小权重。
main 函数：
（图片来源网络，侵删）
- 创建并初始化一个图。
- 为了清晰，先用 INF 填充邻接矩阵,然后手动设置顶点之间的边。
- 调用 primMST 函数，并传入图指针和起始顶点（这里是 0）。

复杂度分析

时间复杂度：
- 使用邻接矩阵实现时，查找最小权重的边需要遍历所有顶点，这部分的时间复杂度是 O(V)。
- 更新 lowcost 和 closest 数组也需要遍历所有顶点，时间复杂度也是 O(V)。
- 这个过程需要执行 V-1 次。
- 总的时间复杂度为 O(V²)。
- 这种实现方式适合于稠密图（边数接近 V² 的图）。
空间复杂度：
- 主要消耗在邻接矩阵上，为 O(V²)。
- 辅助数组 lowcost, closest, visited 的空间复杂度为 O(V)。
- 总的空间复杂度为 O(V²)。

对比 Kruskal 算法

Prim 算法和 Kruskal 算法都是求 MST 的经典算法,但策略不同：

特性	Prim 算法	Kruskal 算法
策略	贪心，从一个顶点开始，向外扩展	贪心，按权重顺序选择边
数据结构	优先队列（或数组）	并查集
时间复杂度	O(E log V) with heap, O(V²) with matrix	O(E log E) ≈ O(E log V)
适用场景	稠密图（边多）	稀疏图（边少）
实现方式	通常从图的一个顶点开始	可以处理不连通的图（得到生成森林）

对于稀疏图，Kruskal 算法通常更高效，对于稠密图，Prim 算法（特别是邻接矩阵实现）可能更简单直接。

prim算法求最小生成树c语言